Ανίχνευση Μη Φυσιολογικής Συμπεριφοράς Λαμβάνοντας Υπόψη την Εγγενή Αβεβαιότητα/ Uncertainty-Aware Detection of Abnormal Behavior

Οι μετρήσεις που λαμβάνονται από ένα δίκτυο αισθητήρων μπορούν να θεωρηθούν αναξιόπιστες και ανακριβείς. Κρίνεται, λοιπόν, αναγκαία η ποσοτικοποίηση της αβεβαιότητας των δεδομένων η οποία μπορεί να λειτουργήσει ως δείκτης για την ποιότητα των μετρήσεων. Οι πηγές αβεβαιότητας σε ένα έξυπνο σύστημα παρακολούθησης υδάτινων πόρων ποικίλουν. Συγκεκριμένα, μπορεί να σχετίζονται με την κατασκευή των αισθητήρων, τις περιβαλλοντικές συνθήκες, τις παρεμβολές, την ποιότητα του μαθηματικού μοντέλου, κ.ά. Ιδιαίτερα στην περίπτωση της ανίχνευσης μη φυσιολογικής συμπεριφοράς από ένα σύνολο λαμβανόμενων μετρήσεων, η συμπερίληψη της εγγενούς αβεβαιότητας στην κατασκευή του αλγορίθμου ευνοεί την ακριβέστερη εκτίμηση ακραίων συμβάντων.

Η λειτουργία ανίχνευσης μη φυσιολογικής συμπεριφοράς έχει εξέχοντα ρόλο στα σύγχρονα έξυπνα συστήματα παρακολούθησης δικτύων υδροδότησης. Στόχος της λειτουργίας αυτής είναι η άμεση και έγκυρη παραγωγή ειδοποιήσεων μη φυσιολογικής συμπεριφοράς, διασφαλίζοντας έτσι την ομαλή λειτουργία του δικτύου. Ο συνυπολογισμός της εγγενούς αβεβαιότητας των καταγεγραμμένων μετρήσεων συντελεί στην έγκαιρη παραγωγή ειδοποιήσεων, καθώς εξετάζεται ένα εύρος δυνατών τιμών για κάθε μέτρηση. Με τη σειρά της, η έγκαιρη παραγωγή ειδοποιήσεων συντελεί στην άμεση λήψη αποφάσεων για την ίαση των μη φυσιολογικών συμβάντων, εξασφαλίζοντας έτσι την αυτονομία του συστήματος. Για παράδειγμα, στην περίπτωση δικτύων υδροδότησης, ως μη φυσιολογική συμπεριφορά ορίζεται η υπέρβαση κάποιων ορίων για τις τιμές μίας φυσικής μεταβλητής (π.χ. πίεση, θερμοκρασία). Σε αντίθεση με την απλή περίπτωση σύγκρισης μιας μέτρησης με τα αντίστοιχα λειτουργικά όρια (δύο περιπτώσεις, υπέρβασης ή μη των ορίων), η συμπερίληψη της αβεβαιότητας στις λαμβανόμενες μετρήσεις οδηγεί σε σύγκριση με τις ακόλουθες τέσσερεις διαφορετικές περιπτώσεις (όπου U συμβολίζει την εκτιμημένη τιμή της αβεβαιότητας):

Περίπτωση 1: (μέτρηση +/- U) εκτός ορίων
Περίπτωση 2: μέτρηση εκτός ορίου και (μέτρηση – U) εντός ορίου
Περίπτωση 3: μέτρηση εντός ορίων και (μέτρηση + U) εκτός ορίου
Περίπτωση 4: (μέτρηση +/- U) εντός ορίων

The measurements recorded by a network of sensors can be considered unreliable and inaccurate. It is, therefore, necessary to quantify the uncertainty of the observed data, which can be used as an indicator of the measurements’ quality. In a smart water monitoring system the potential sources of uncertainty may vary. In particular, they can be related with the sensor’s manufacturing, the environmental conditions, the presence of interference, the quality of the mathematical models, etc. In the specific case of detection of abnormal behaviors based on the recorded data, accounting for the inherent uncertainty in the algorithmic design typically improves the accuracy in detecting extreme events.

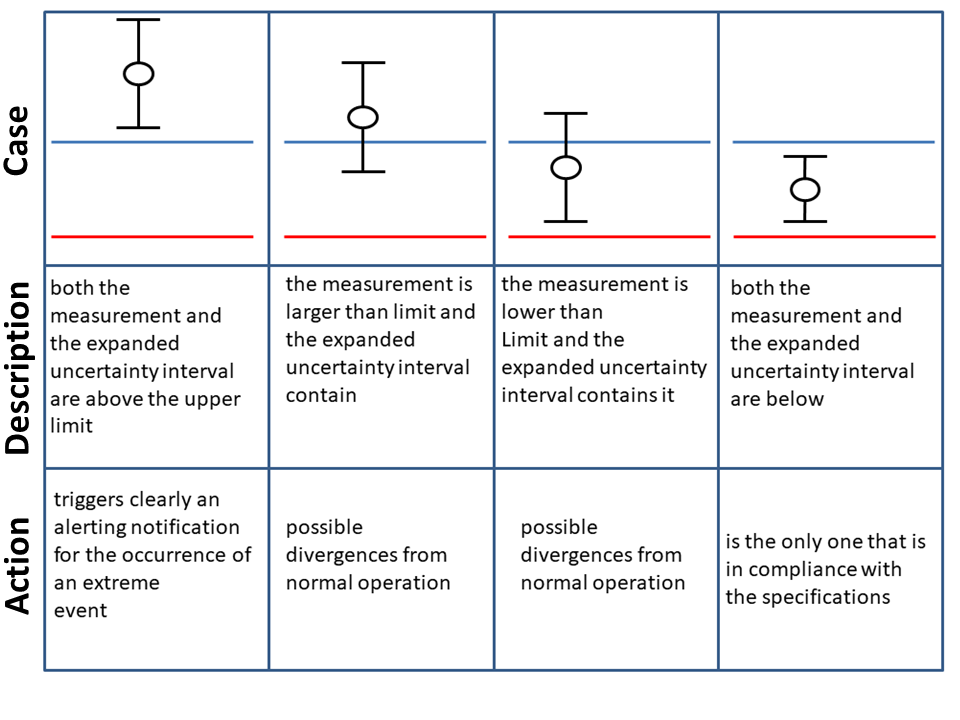
The functionality of abnormal behaviors’ detection has a prominent role in the modern systems for smart monitoring of water distribution networks. The objective of this functionality is the timely and accurate production of notifications for the occurrence of abnormal behaviors, thus guaranteeing the smooth operation of the water network. Accounting for the inherent data uncertainty yields the timely generation of alerts, since a range of potential values for each individual recorded measurement is examined. In turn, the timely production of alerts enables fast decision-making to remedy the effects of extreme events, ensuring the system’s autonomous operation. For instance, in the case of water distribution networks, an abnormal behavior is defined as the exceedance of predetermined operational limits for the values of a physical quantity (e.g. pressure, temperature). In contrast to the naïve case where a measurement is compared with the corresponding operational limits (two cases of exceeding or not the limits), accounting for the inherent uncertainty in the received measurements yields a comparison with four distinct cases, as follows (U denotes the estimated uncertainty value):

Case 1: (measurement +/- U) out of limits
Case 2: measurement outside limits and (measurement – U) within limit
Case 3: measurement within limits and (measurement + U) outside limits
Case 4: (measurement +/- U) within limits