Συμπιεστική Δειγματοληψία/ Compressive Sensing

Ένας περιορισμός που απαντάται συχνά στα ασύρματα δίκτυα αισθητήρων είναι τα περιορισμένα αποθέματα της μπαταρίας. Η μείωση του όγκου των δεδομένων που αποστέλλονται από τους αισθητήρες έχει διπλό ρόλο: αφενός αυξάνει την αυτονομία του συστήματος και αφετέρου μειώνει το κόστος τηλεμετρίας εξαιτίας του περιορισμένου όγκου δεδομένων που αποστέλλονται. Σε ένα σύστημα διαχείρισης υδάτινων πόρων, κρίσιμο ζήτημα αποτελεί επίσης η εμπιστευτικότητα των δεδομένων. Όταν, για παράδειγμα, περιλαμβάνονται δεδομένα κατανάλωσης από οικιακούς μετρητές. Οι παραπάνω στόχοι μπορούν να επιτευχθούν με χρήση της τεχνικής συμπιεστικής δειγματοληψίας η οποία επιτυγχάνει υψηλή συμπίεση των δεδομένων καθώς και την ταυτόχρονη κρυπτογράφησή τους.

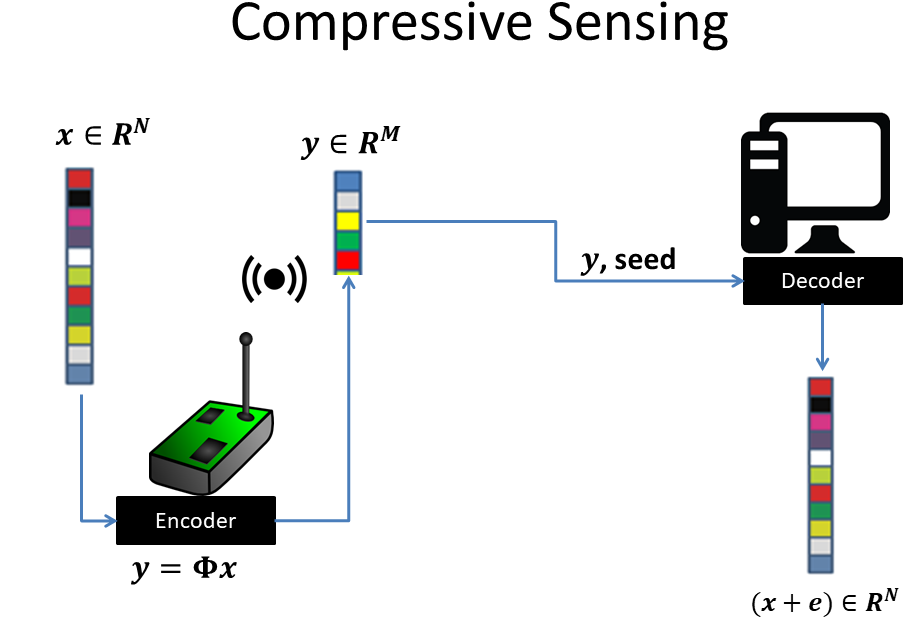
Η συμπιεστική δειγματοληψία πραγματοποιείται σε δυο επίπεδα: στα άκρα του δικτύου και στο κέντρο ελέγχου. Αρχικά, εφαρμόζεται η συμπίεση των δεδομένων στα άκρα του δικτύου. Έστω x το αρχικό διάνυσμα δεδομένων μήκους Ν. Το συμπιεσμένο διάνυσμα y μήκους Μ δίνεται από τη σχέση y = Φ·x. Ο πίνακας Φ, διαστάσεων MxN, μοντελοποιεί τη διαδικασία γραμμικής υποδειγματοληψίας. Μερικά παραδείγματα πινάκων που εγγυώνται την ακριβή ανακατασκευή του αρχικού διανύσματος x από τις συμπιεσμένες μετρήσεις y αποτελούν πίνακες των οποίων τα στοιχεία επιλέγονται τυχαία από Gaussian, Bernoulli, κ.ά. κατανομές. Στο κέντρο ελέγχου πραγματοποιείται η αποσυμπίεση των δεδομένων προκειμένου να επεξεργαστούν. Η αποσυμπίεση των δεδομένων πραγματοποιείται επιλύοντας κατάλληλα προβλήματα (κυρτής ή μη-κυρτής) βελτιστοποίησης δοθέντος του περιορισμού y = Φ·Ψ·v, όπου y είναι το διάνυσμα των συμπιεσμένων μετρήσεων, Φ ο πίνακας δειγματοληψίας, και Ψ ένας μετασχηματισμός αραιοποίησης του αρχικού διανύσματος x σε μια Κ-αραιή (από τα Ν στοιχεία, μόνο τα Κ είναι διαφορετικά του μηδενός) αναπαράσταση v. Στην υλοποίησή μας στα πλαίσια του SmartWater2020, χρησιμοποιείται ο short-Time Fourrier Transform (SFTF) ως μετασχηματισμός αραιοποίησης, ενώ για την ανακατασκευή του αρχικού διανύσματος x χρησιμοποιείται ο αλγόριθμος NESTA (https://statweb.stanford.edu/~candes/nesta/).

A limitation often encountered in wireless sensor networks is the limited battery capacity. Reducing the amount of data sent by the sensors has a dual role: on the one hand, it increases the autonomy of the system and, on the other hand, it reduces telemetry costs due to the limited volume of data to be transmitted. In a water management system, data confidentiality is also a critical issue. When, for instance, consumption data from home meters are included. The above objectives can be achieved exploiting the framework of compressive sensing, which achieves high data compression and simultaneous encryption.

Compressive sensing is performed in two stages: at the edges of the network and at the control center. First, data compression is carried out at the edges of the network. Let x be the original data vector of length N. The compressed vector y of length M is given by the relation y = Φ·x. The matrix Φ, of dimension MxN, models the linear subsampling process. Examples of such matrices that guarantee an accurate reconstruction of the original vector x from the compressed measurements y include matrices whose elements are drawn from a Gaussian, Bernoulli, etc. distributions. At the control center, decompression/reconstruction of the data takes place to be further processed. Data decompression is performed by solving appropriate (convex or non-convex) optimization problems given the constraint y = Φ·Ψ·v, where y is the vector of compressed measurements, Φ is the sampling matrix, and Ψ a sparsifying transformation of the original vector x into a K-sparse (only K out of the N samples are nonzero) representation v. In our implementation in the framework of SmartWater2020, the Short-Time Fourrier Transform (SFTF) is employed as the sparsifying transformation, whilst the NESTA algorithm is used for the reconstruction of the original vector x (https://statweb.stanford.edu/~candes/nesta/).